개념
평면 상에서 좌표를 알고 있는 한 점에서 두 점의 좌표를 알고있는 직선에 가장 가까운 위치의 좌표를 구하는 방법을 알아본다.

먼저 한 점이 직선에 이르는 가장 가까운 위치는 해당 점에서 직선까지 수선을 내렸을 때 교차하는 지점이다. 따라서 해당 지점을 구하기 위해서는 직선에 수직이면서 한 점(C 지점)을 지나는 새로운 직선과 원래 존재하던 직선의 교점을 구하면 된다.
풀이
A,B점을 포함하는 직선과 수직인 직선의 기울기는 A, B점의 기울기의 역수의 음의 값이다. 먼저 A,B 점을 포함하는 직선의 기울기 a 는 아래와 같다.

해당 값의 역수의 음수 값이 A, B 점을 포함하는 직선에 수직인 직선의 기울기가 된다. 해당 값과 해당 직선의 방정식은 아래와 같다.
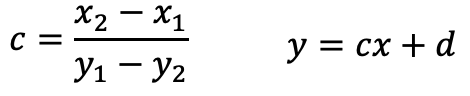
해당 직선은 한 점 C를 지나기 때문에 C의 좌표값을 대입해 상수 d의 값도 구해낸다. 계산을 마치고 나온 점 C를 지나고 A, B점을 포함하는 직선에 수직인 직선의 방정식은 아래와 같다.

위의 직선이 A, B점을 포함하는 직선과 만나는 지점이 최단거리가 발생하는 지점이기 때문에 A, B 점을 포함하는 직선의 방정식을 구해, 위의 방정식과 연립하여 교차점의 x, y 좌표를 구해준다.


'잡동사니 > 기하학' 카테고리의 다른 글
| 임의의 다각형 또는 꺾인 선으로 곡선 만들기 - Chaikin's Algorithm (0) | 2023.02.22 |
|---|---|
| 직선과 원이 만나는 지점의 좌표 구하기 (0) | 2023.02.18 |
| 한 직선에 수직인 직선의 기울기 (0) | 2023.02.18 |
| 2점을 지나는 직선의 방정식 (0) | 2023.02.15 |
| 3점을 지나는 원의 방정식 (0) | 2023.02.15 |




댓글